Lattice Visualisation
Running an example LatticeView example1. For defining the dataset follow the example below. Notice that columns are separated by tabs. In the example, columns represent attributes while rows objects. An x in a cell means that the object has the property indicated by the column.
| data fca context |
data :='
a b c d e f g h
1 x x x
2 x x x
3 x x x
4 x x x
5 x x x
6 x x x
7 x
8 x x
9 x x x
10 x x x
11 x x x
12 x x x
13 x x x
14 x x x
15 x x x
16 x x x
17 x x x
18 x x
19 x x
20 x x x
21 x x x
22 x x x
23 x x
24 x x x
25 x x x
26
27 x
28 x
29 x
30 x
31 x
32 x x'.
fca := MalFormalContext new.
context := fca with: (LatticeUtil formatData: data) using: #first using: #last.
lattice := MalLattice on: context.
(LatticeView new
on: lattice nodes;
entitiesBlock: [:e| e model objects];
propertiesBlock: [:e| e model attributes];
layerBlock: [:e| e model attributes size];
edgesToAllBlock: [:e| e descendants];
edgesFromAllBlock: [ :e | e anscentorLabel ];
nodesSize: [ :e | e model objects size ];
nodesColor: [ :e | Color random ];
popUp: [ :e | e name ];
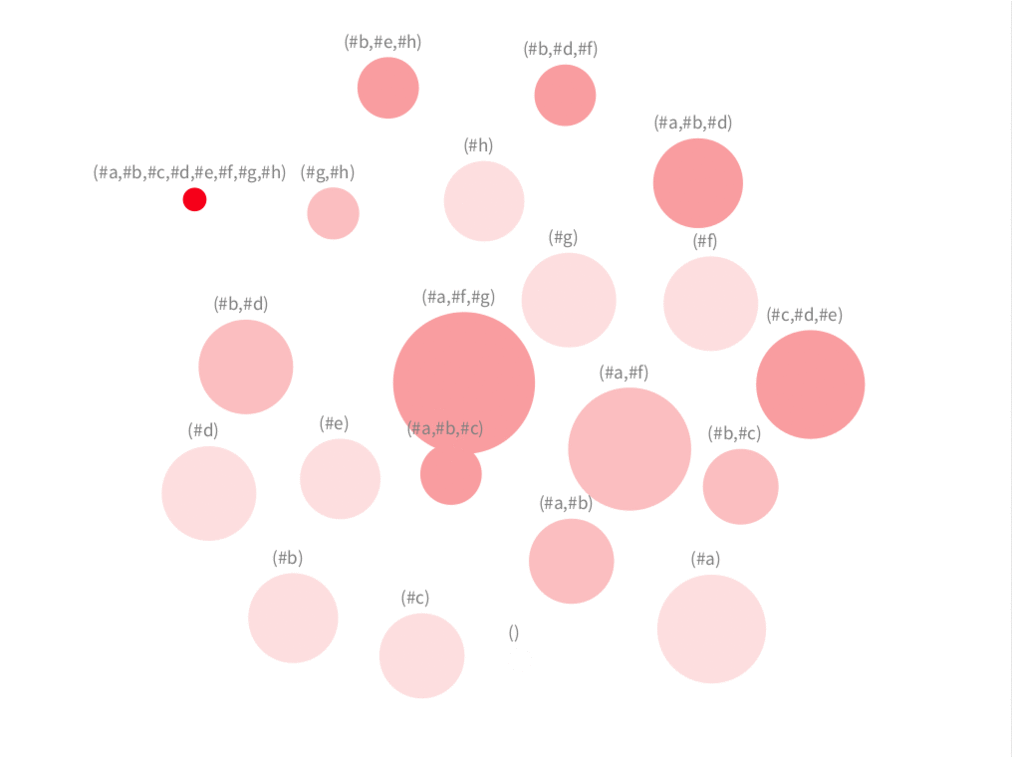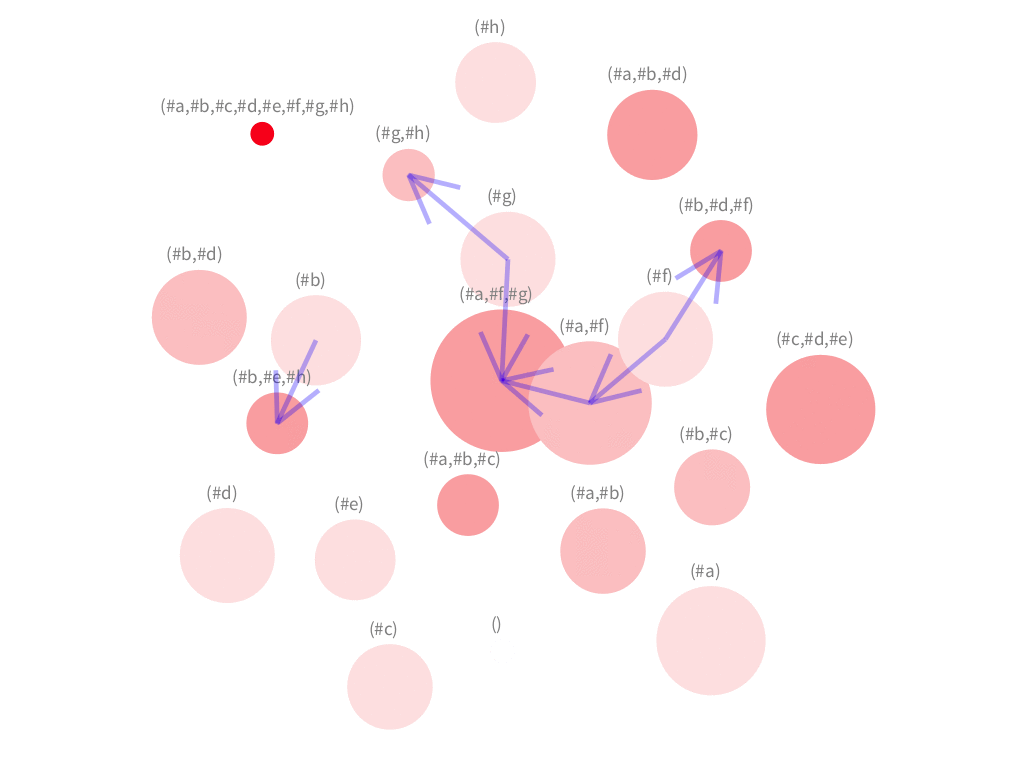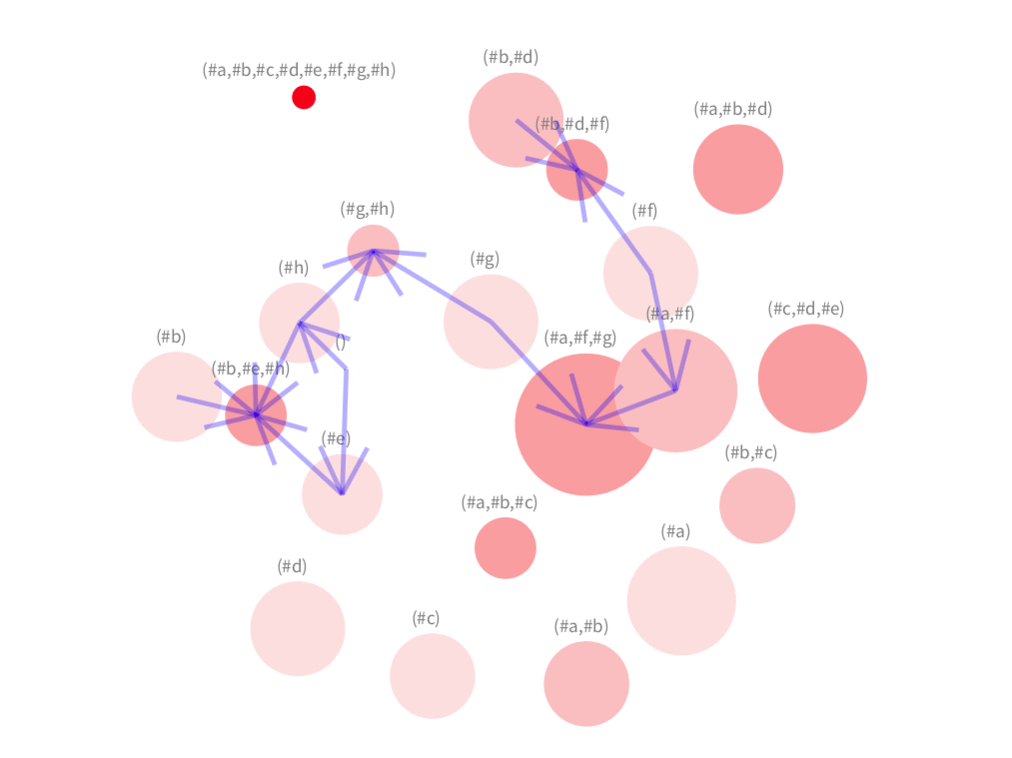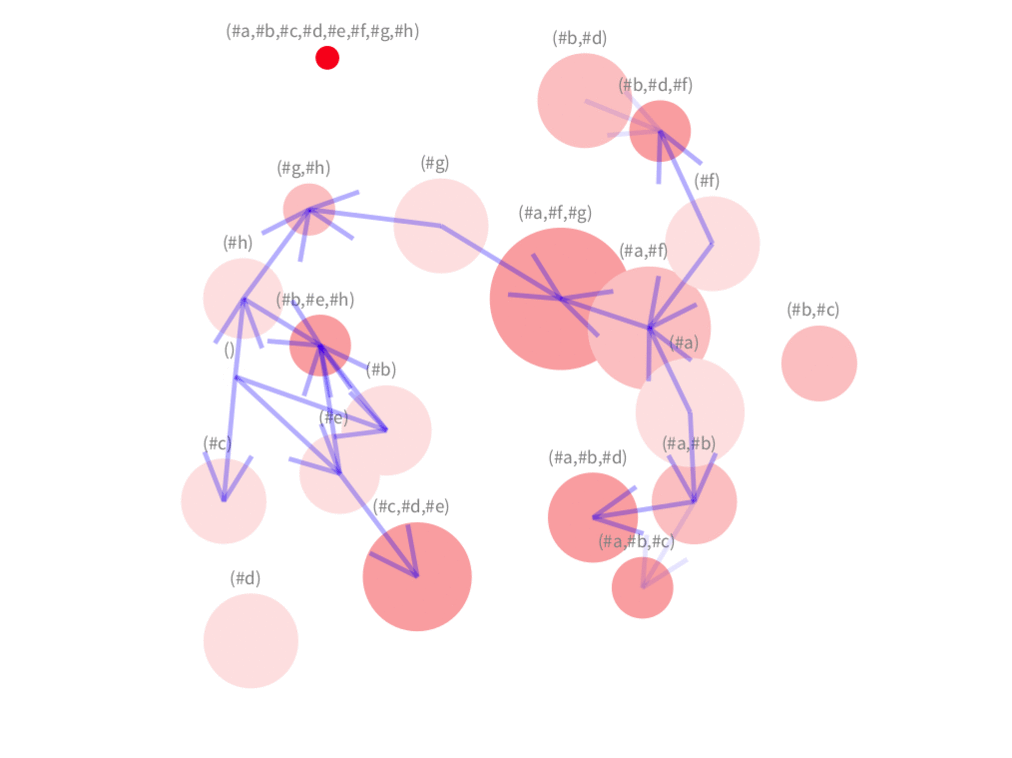
label: #name) Figure 1. Galois Lattice of layered Hasse diagrams.
Figure 1. Galois Lattice of layered Hasse diagrams.
Each circle represents a concept (which holds a set of objects and attributes). The size of the circle is the product of its number of attributes by its number of objects. Doing so, the visualisation highlights concepts that not only have many objects but also have many attributes. The intensity of the color is mapped to the number of attributes of the concept.
The attributes of a concept are the union of the attributes of the concepts from which its incoming arrows come from. Similarly, the attributes of a concept are the intersection of the attributes of the concepts defined by the endpoint of its outgoing arrows. As shown in the Figure below.
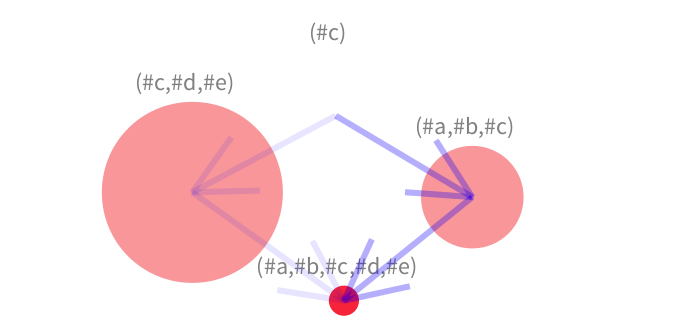
In the example we introduced four cases:
- Objects 2-6 have attributes (#c,#d,#e). Object 7 only has attribute (#e).
- Objects 9-17 have attributes (#a,#f,#g), while object 18 only has attributes (#a,#f).
- Objects 20-22 have attributes (#a,#b,#d), while objects (23,24) only have attributes (#b,#d).
- Objects 27-31 have attribute (#h), while object 32 has attributes (#g,#h).
Our goal in all cases is to detect the (primary) concept that clustered the main group of objects, but also the (secondary) concept that clustered the remaining close objects. Note that in the first three cases the secondary cluster will contain a subset of attributes of the primary concept; while in the last case the secondary concept will contain a superset.
The Hasse diagram of the Galois Lattice can be useful by depicting the concepts and showing their relationships by edges. However, it does not scale well. The number of concepts grows exponentially respect the number of attributes. Therefore, the number of edges can make very difficult to extract useful information in a large Lattice.
We believe that for our purpose we do need to see all concepts for detecting the ones that clustered the most of objects; but we really do not need to see all edges. In fact, a visualisation that would show us only the edges from the secondary concepts to the primary ones would benefit our analysis.
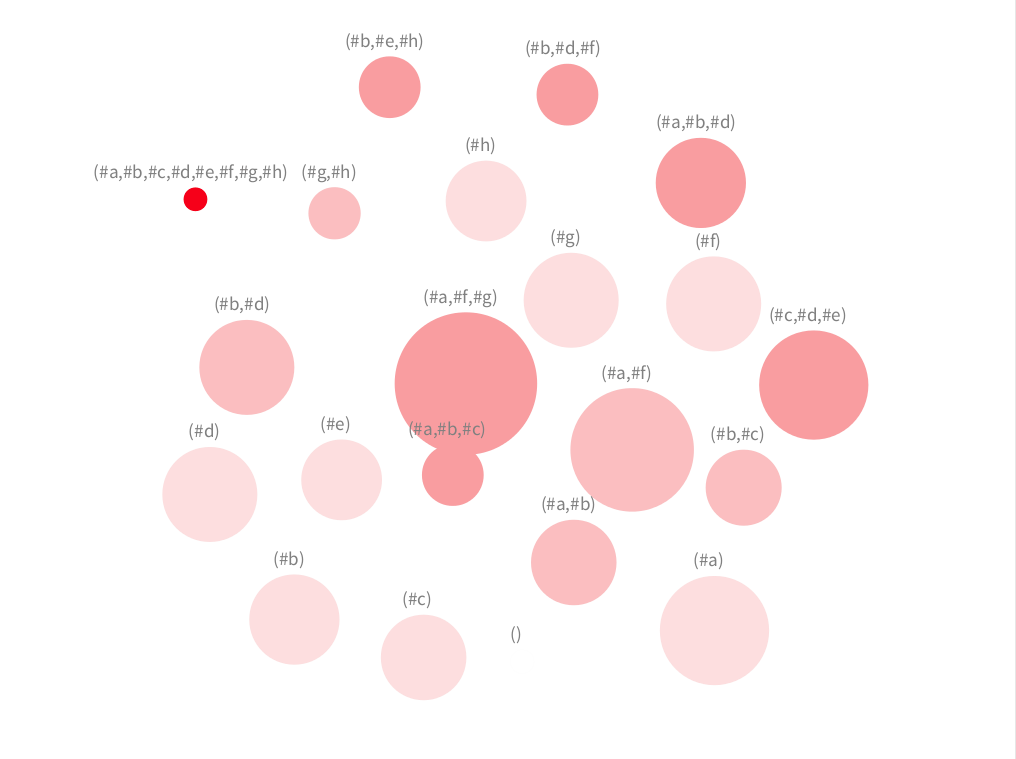
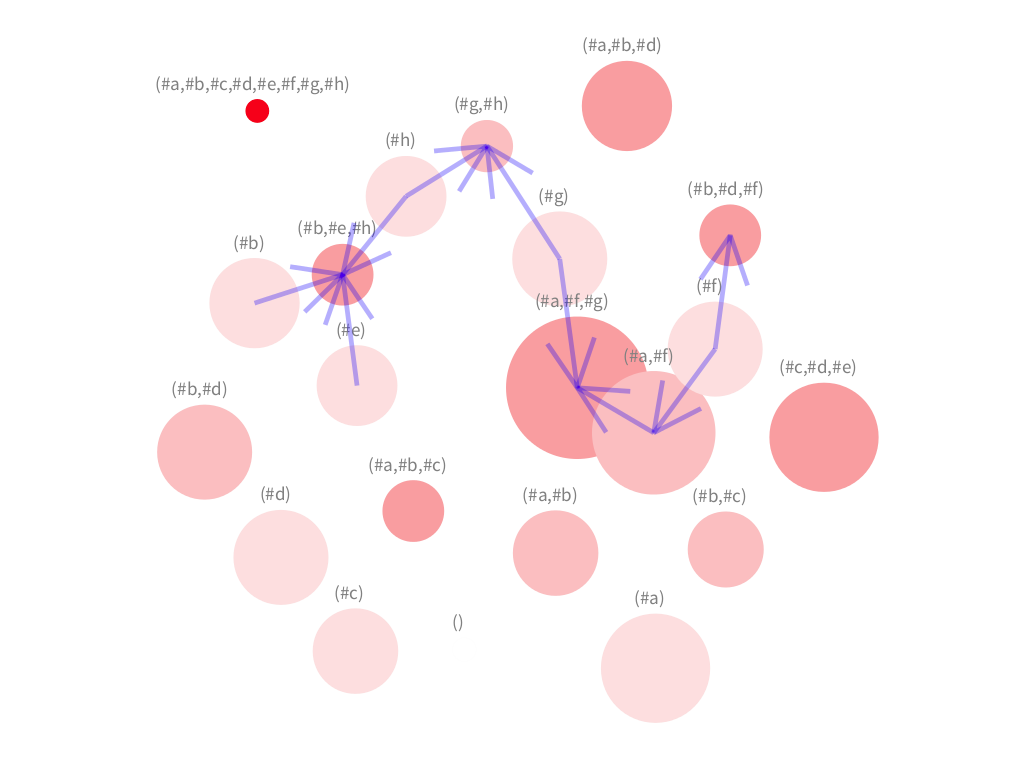
A force-directed (strong clustering) layout seems better when having only some of edges of a graph of an unknown structure. Our visualisation allows the user to add and remove interactively edges, which can be seen in the animation below. The user starts we a visualisation that shows only the concepts. Afterwards the user can add edges incrementally. The set of edges shown are selected from pair of concepts where their number of attributes differ in a certain threshold that the user can define. Therefore, adding more edges means that the user is lowering the threshold (while removing edges means the opposite).
In this first view, the user can detect the primary concepts, which are represented by the largest circles. That is the case of concepts holding attributes (#c,#d,#e), (#a,#f,#g), (#a,#b,#d). Notice that the case four (#h) is not detected because the number of objects and attributes is low (false negative).
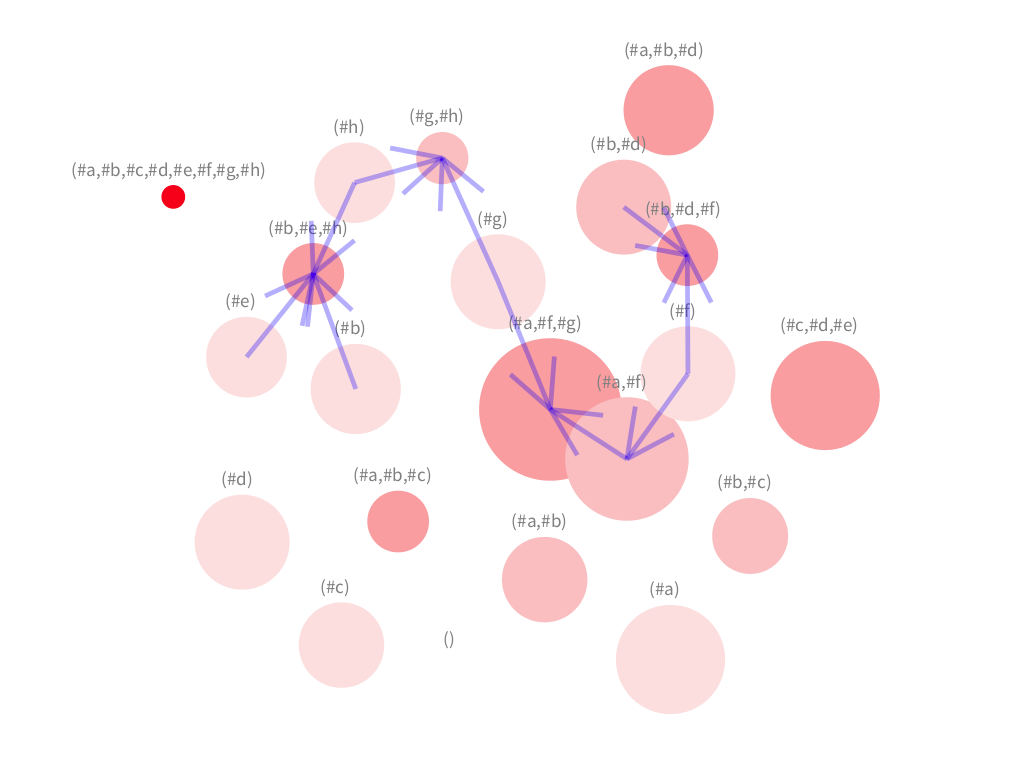
In this first iteration, some edges appear around concept (#a,#f,#g). In fact, we can easily detect the concept (#a,#f) represented by a large circle close to it.
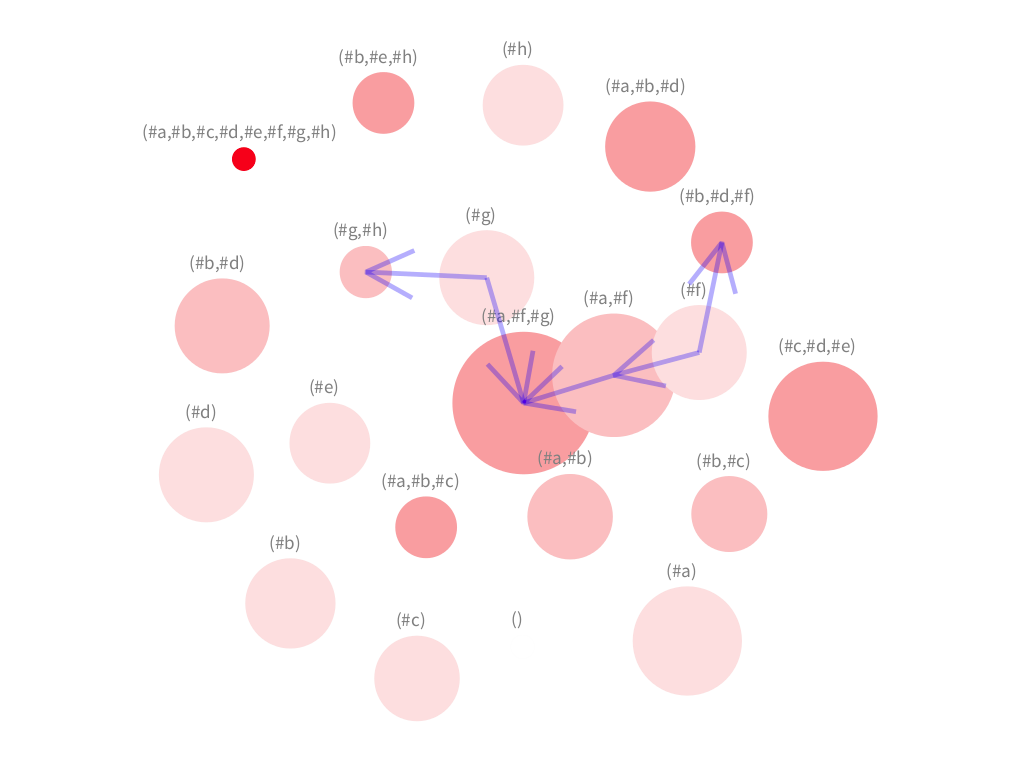
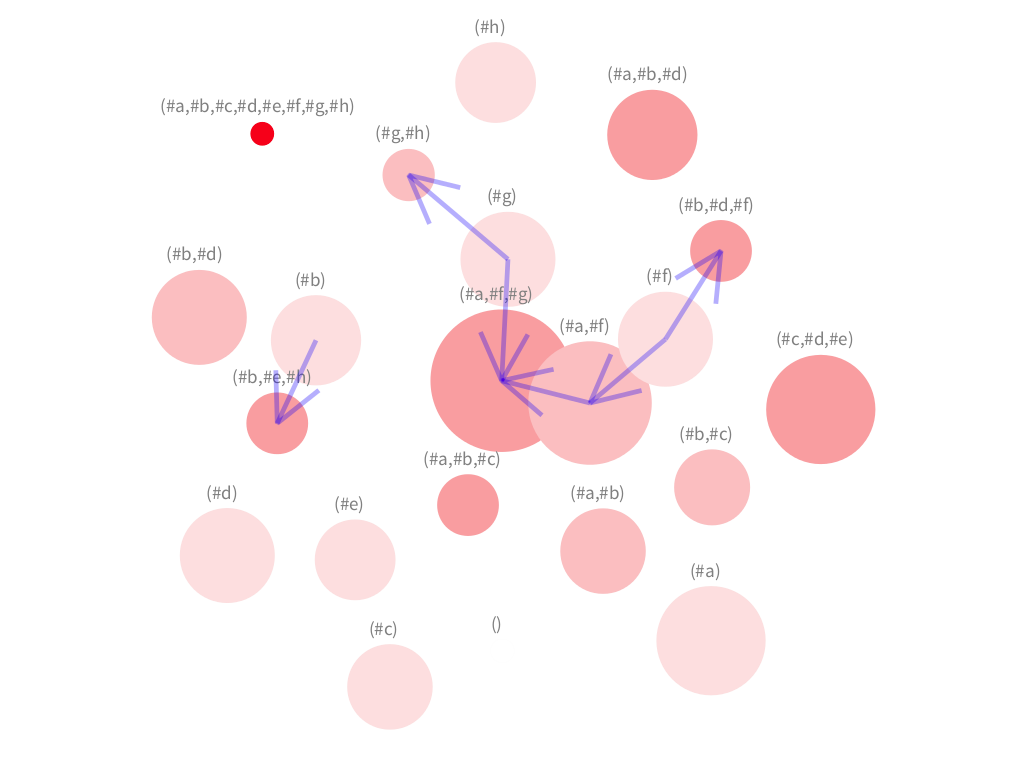
Here concept (#h) is reached by an edge. However, the visualisation does not provide much insight here.
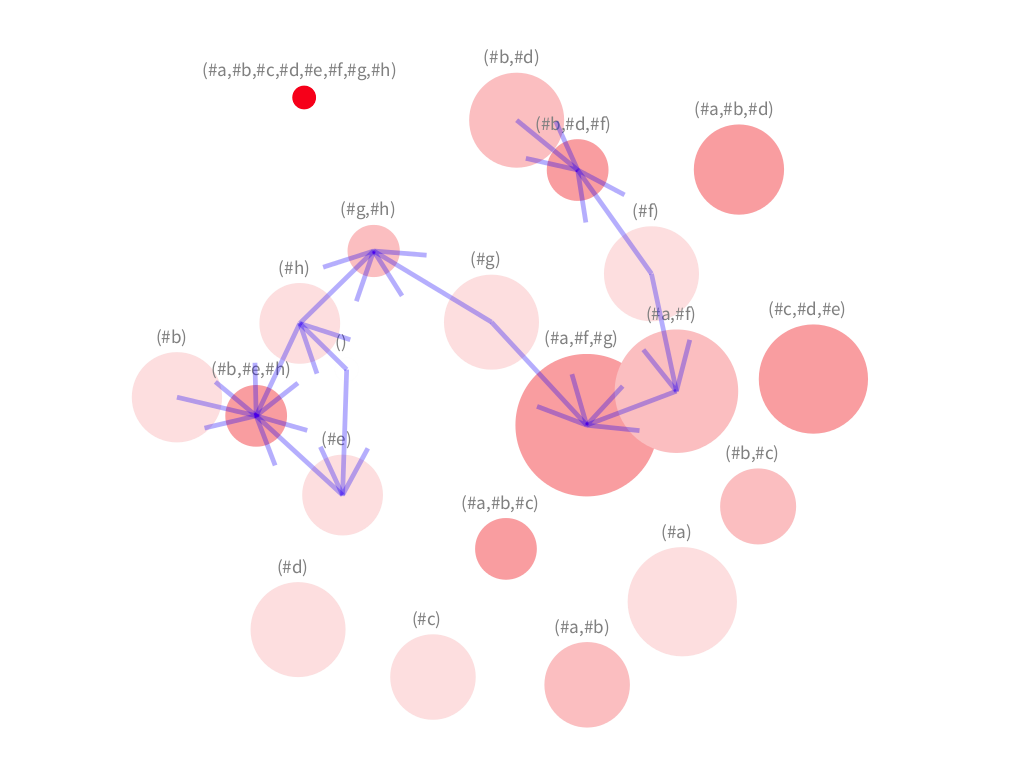
- Here we notice an edge connecting the primary concept (#a,#d,#b) with the secondary (#b,#d).
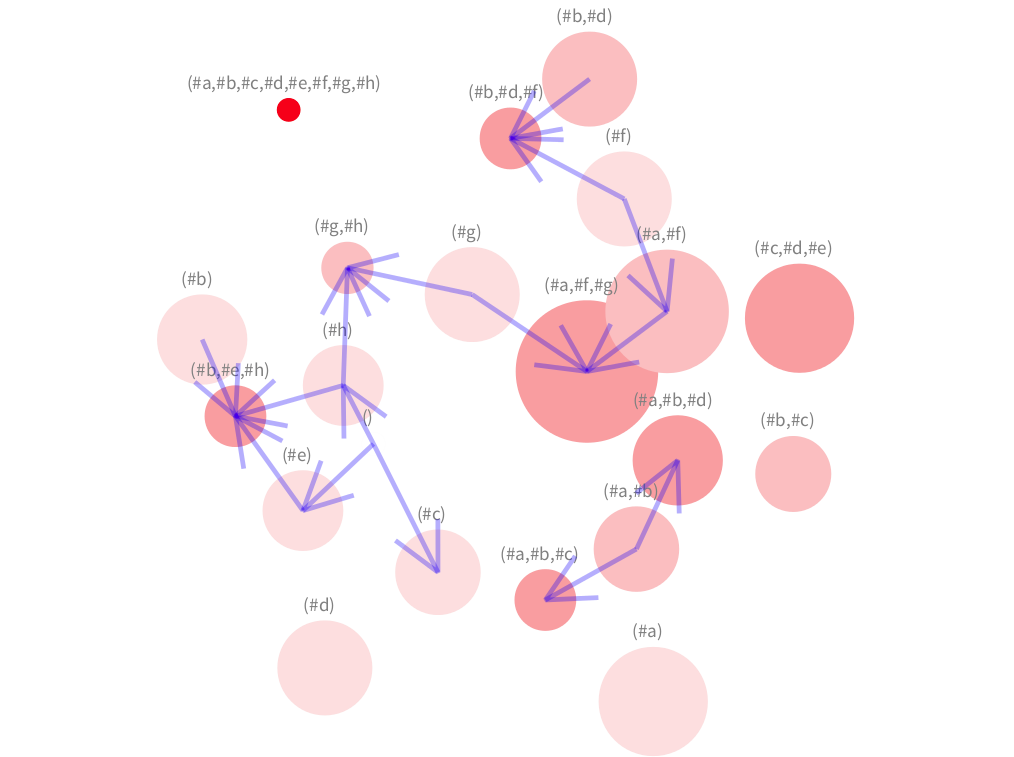
Finally, an edge connects the primary concept (#c,#d,#e) to the secondary concept (#e).

Notice that trying this very small example in the Hasse diagram of Figure 1 seems much more complex.
Installation
Pharo 4.0.2
-
Install Roassal through the Configuration Browser
-
Install MooseAlgos
Gofer new smalltalkhubUser: 'Moose' project:'MooseAlgos'; configuration; load. (Smalltalk at: #ConfigurationOfMooseAlgos) loadStable -
Install LatticeView
Gofer new package: 'ConfigurationOfLattice'; url: 'http://smalltalkhub.com/mc/merino/LatticeView/main' username: '' password: ''; update. (Smalltalk at: #ConfigurationOfLattice) loadDefault
Moose 6.0 stable image.
Since Moose already includes Roassal and MooseAlgos installed you only need to do the step 3 from above.
 Animation of a sequence when visualising a Lattice.
Animation of a sequence when visualising a Lattice.